Assalamu'alaikum teman teman semua,,,,
apa kabarnya ???  semoga Allah melindungi kita semua ....

untuk kali ini, penulis akan menyajikan soal latihan tentang pertidaksamaan linear dua variabel..

1. Gambarlah daerah penyelesaian sistem pertidaksamaan x + 2y > -4, 2x – y ≤ 3 dengan mengarsir daerah penyelesaian!
2. Gambarlah daerah penyelesaian sistem pertidaksamaan x ≥ 0 ; x + y ≥ 3 ; 2x + y ≤ 4 dengan mengarsir daerah penyelesaian!
3. himpunan penyelesaian dari : 3x-2 ≥ 4x+6, x ∈ B adalah ...
4. Tentukan himpunan penyelesaian dari sistem persamaan x + 2y = 7; x,y∈R dan 2x + 3y = 10; x,y∈R ...
5. Tentukan himpunan penyelesaian dari sistem persamaan 2x – y = –2; x,y Î R dan x + 2y = 4; x,y Î R ...

gimana teman-teman? mudah bukan soal-soal yang sudah diberikan. Semoga bermanfaat

Contoh soal dan pembahasan sistem pertidaksamaan linear dua variabel

Assalamu'alaikum teman teman semua,,,,
apa kabarnya ???  semoga Allah melindungi kita semua ....

untuk kali ini, penulis akan menyajikan contoh soal dan pembahasan tentang pertidaksamaan linear dua variabel.
Pertidaksamaan linier dua variabel yaitu suatu pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi satu.
Penyelesaian dari pertidaksamaa linier dua variabel ini merupakan gambar daerah pada grafik Catesius (sumbu-XY) yang dibatasi oleh suatu garis linier

Untuk lebih jelasnya ikutilah contoh soal berikut ini :

01. Tentukanlah daerah penyelesaian pertidaksamaan linier 2x + y ≤ 6, dengan x dan y anggota real.
Jawab
Pertama kita lukis garis 2x + y = 6 dengan bantuan tabel.

Selanjutnya diambil satu titik sembarang sebagai titik uji, misalnya O(0, 0), sehingga diperoleh 2(0) + 0 = 0 ≤ 6

Jadi himpunan penyelesaiannya adalah daerah bagian kiri bawah garis 2x + y = 6.

Jika beberapa pertidaksamaan linier bergabung dalam satu sistem, maka bentuk tersebut dinamakan sistem pertidaksamaan linier, dimana himpunan penyelesaiannya merupakan irisan dari daerah penyelesaian masing-masing pertidaksamaan linier.

Untuk pemahaman lebih lanjut akan diuraikan pada contoh soal berikut ini

02. Tentukanlah daerah penyelesaian dari sistem pertidaksamaan linier :
2x + 3y ≤ 12 , x ≥ 1 , y ≥ 1

Jawab
Pertama akan dilukis garis 2x + 3y = 6, garis x= 1 dan garis y = 1 ke dalam satu tatanan koordinat Cartesius

Himpunan penyelesaiannya adalah daerah segitiga yang bebas dari arsiran.

03. Tentukanlah sistem pertidaksamaan untuk dearah yang diarsir pada gambar di bawah ini.

Untuk menentukan sistem pertidaksamaan pada gambar di atas, harus ditentukan terlebih dahulu persamaan garis lurus yang menjadi batas-batas daerahnya, yakni dengan menggunakan rumus :

Sehingga sistem pertidaksamaan linier untuk gambar di atas adalah :

3x + 2y ≤ 12

x + 2y ≤ 8

x ≥ 0

y ≥ 0

Catatan : Jika kedua titik yang terletak pada garis lurus tersebut, diketahui berada pada sumbu-X dan sumbu-Y,

04. Tentukanlah sistem pertidaksamaan untuk dearah yang diarsir pada gambar di bawah ini.

Jawab
Persamaan garis yang melalui titik (4,0) dan (0, 3) adalah

Persamaan garis yang melalui titik (4,0) dan (0, -2) adalah

Sehingga sistem pertidaksamaan linier untuk gambar di atas adalah :
3x + 4y ≤ 12
x – 2y ≤ 4
x ≥ 0

gimana? mudah kan belajar sistem pertidaksamaan linear dua variabel. 

Sistem Pertidaksamaan Linear Dua Variabel

Pertidaksamaan Linear Dua Variabel


Assalamu'alaikum teman teman semua,,,,
apa kabarnya ???  semoga Allah melindungi kita semua ....

untuk kali ini, penulis akan menyajikan materi tentang pertidaksamaan linear dua variabel.


Pertidaksamaan linear dua variabel adalah kalimat terbuka matematika yang memuat dua variabel, dengan masing-masing variabel berderajat satu dan dihubungkan dengan tanda ketidaksamaan. Tanda ketidaksamaan yang dimaksud adalah >, <, ≤, atau ≥. Sehingga bentuk pertidaksamaan linear dapat dituliskan sebagai berikut.
ax + by > c
ax + by < c
ax + by ≥ c
ax + by ≤ c


Dengan :
a = koefisien dari x, a ≠ 0
b = koefisien dari y, b ≠ 0
c = konstanta
a, b, dan c anggota bilangan real.

Penyelesaian dari suatu pertidaksamaan linear dua variabel berupa pasangan terurut (a, b) yang memenuhi pertidaksamaan linear dua variabel. Semua penyelesaian dari pertidaksamaan linear dua variabel disatukan dalam suatu himpunan penyelesaian. Himpunan penyelesaian dari suatu
pertidaksamaan linear dua variabel biasanya disajikan dalam bentuk grafik pada bidang koordinat cartesius. Langkah-langkah yang harus diambil untuk menggambar kan grafik penyelesaian dari per tidaksama an linear dua variabel, hampir sama dengan langkah-langkah dalam menggambarkan grafik persamaan linear dua variabel.


Berikut adalah contohnya
2x + 3y > 6
4x - y < 9

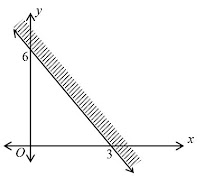
Berbeda dengan penyelesaian dari persamaan linear dua variabel yang berupa himpunan pasangan titik-titik atau jika digambar grafiknya akan berupa garis lurus, penyelesaian pertidaksamaan linear dua variabel berua daerah penyelesaian. Dalam praktiknya penyelesaian pertidaksamaan linear dapat berupa daerah diarsir atau sebaliknya daerah penyelesaian pertidaksamaan linear dua variabel berupa daerah bersih.

Untuk menentukkan daerah penyelesaiannya, dapat dilakukan melalui langkah-langkah berikut.

1. Ubahlah tanda ketidaksamaan dari pertidaksamaan menjadi tanda sama dengan (=), sehingga diperoleh persamaan linear dua variabel
2. Lukis grafik/garis dari persamaan linear dua variabel tadi. Hal ini dapat dilakukan dengan menentukan titik potong sumbu x dan sumbu y dari persamaan atau menggunakan dua titik sembarang yang dilalui oleh garis. Garis akan membagi dua bidang kartesius
3. Lakukan uji titik yang tidak dilalui oleh garis (substitusi nilai x dan y titik ke pertidaksamaan). Jika menghasilkan pernyataan yang benar, artinya daerah tersebut merupakan penyelesaiannya, namun apabila menghasilkan pernyataan salah maka bagian lainnya lah yang merupakan penyelesaiaanya.

Gimana? Membantu tidak?

Sekian materi tentang sistem pertidaksamaan linear dua variabel yang saya sampaikan. 

Saya adalah seorang laki-laki yang lahir di Tangerang pada tanggal 18 November 2002, diberi nama Faiq Alfadhillah Romadhon. Kedua orang tua saya bernama Supriyadi dan Maya Susanti. Saya anak 1 dari 2 bersaudara. Sejak kecil saya tinggal di kabupaten Tangerang, menamatkan sekolah di SDN Kutajaya 2  dan SMPN 2 Kecamatan Pasarkemis. Hobi saya adalah foto bus di pinggir jalan dan di terminal. Saya sangat senang dengan bus Po Haryanto.